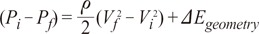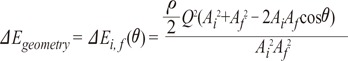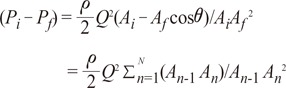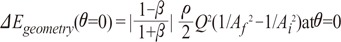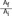1. Chen J, Lu XY. Numerical investigation of the non-Newtonian blood flow in a bifurcation model with a non-planar branch. J Biomech 2004;37:1899-1911 .


2. Olufsen MS, Peskin CS, Kim WY, Pedersen EM, Nadim A, Larsen J. Numerical simulation and experimental validation of blood flow in arteries with structured-tree outflow conditions. Ann Biomed Eng 2000;28:1281-1299 .


3. Darne B, Girerd X, Safar M, Cambien F, Guize L. Pulsatile versus steady component of blood pressure: a cross-sectional analysis and a prospective analysis on cardiovascular mortality. Hypertension 1989;13:392-400 .


4. Johnson DA, Spaeth JR, Rose WC, Naik UP, Beris AN. An impedance model for blood flow in the human arterial system. Part i: Model development and matlab implementation. Comput Chem Eng 2011;35:1304-1316.

8. Oh TS, Ko YB, Park ST, Yoon KH, Lee SW, Park JW, et al. Computational flow dynamics study in severe carotid bulb stenosis with ulceration. Neurointervention 2010;5:97-102.

9. Shojima M, Oshima M, Takagi K, Torii R, Hayakawa M, Katada K, et al. Magnitude and role of wall shear stress on cerebral aneurysm: computational fluid dynamic study of 20 middle cerebral artery aneurysms. Stroke 2004;35:2500-2505 .


10. Xiang J, Natarajan SK, Tremmel M, Ma D, Mocco J, Hopkins LN, et al. Hemodynamic-morphologic discriminants for intracranial aneurysm rupture. Stroke 2011;42:144-152 .


11. Luo B, Yang X, Wang S, Li H, Chen J, Yu H, et al. High shear stress and flow velocity in partially occluded aneurysms prone to recanalization. Stroke 2011;42:745-753 .


12. Takao H, Murayama Y, Otsuka S, Qian Y, Mohamed A, Masuda S, et al. Hemodynamic differences between unruptured and ruptured intracranial aneurysms during observation. Stroke 2012;43:1436-1439 .


13. Johnston BM, Johnston PR, Corney S, Kilpatrick D. Non-Newtonian blood flow in human right coronary arteries: steady state simulations. J Biomech 2004;37:709-720 .


14. Gijsen FJ, van de Vosse FN, Janssen JD. The influence of the non-Newtonian properties of blood on the flow in large arteries: steady flow in a carotid bifurcation model. J Biomech 1999;32:601-608 .


15. Molla MM, Paul MC. LES of non-Newtonian physiological blood flow in a model of arterial stenosis. Med Eng Phys 2012;34:1079-1087 .


16. Fisher C, Rossmann JS. Effect of non-Newtonian behavior on hemodynamics of cerebral aneurysms. J Biomech Eng 2009;131:091004.


17. Kim YH, Xu X, Lee JS. The effect of stent porosity and strut shape on saccular aneurysm and its numerical analysis with lattice Boltzmann method. Ann Biomed Eng 2010;38:2274-2292 .


18. Vignon-Clementel IE, Figueroa CA, Jansen KE, Taylor CA. Outflow boundary conditions for 3D simulations of non-periodic blood flow and pressure fields in deformable arteries. Comput Methods Biomech Biomed Engin 2010;13:625-640 .


19. Salvi P, Bellasi A, Di Iorio B. Does it make sense to measure only the brachial blood pressure? Blood Purification 2013;36:21-22 .


20. Weber T, Auer J, O'Rourke MF, Kvas E, Lassnig E, Berent R, et al. Arterial stiffness, wave reflections, and the risk of coronary artery disease. Circulation 2004;109:184-189 .


21. Nichols W, O'Rourke MF. Mcdonald's blood flow in arteries: Theoretical, experimental, and clinical principles, : London, Edward Arnold; 1998.
22. Passerini T, Sangalli L, Vantini S, Piccinelli M, Bacigaluppi S, Antiga L, et al. An integrated statistical investigation of internal carotid arteries of patients affected by cerebral aneurysms. Cardiovasc Eng Technol 3:26-40.

24. Qian Y, Liu J, Itatani K, Miyaji K, Umezu M. Computational hemodynamic analysis in congenital heart disease: simulation of the norwood procedure. Ann Biomed Eng 2010;38:2302-2313 .


25. Akins CW, Travis B, Yoganathan AP. Energy loss for evaluating heart valve performance. J Thorac Cardiovasc Surg 2008;136:820-833 .


26. Ascuitto RJ, Kydon DW, Ross-Ascuitto NT. Streamlining fluid pathways lessens flow energy dissipation: relevance to atriocavopulmonary connections. Pediatr Cardiol 2003;24:249-258 .


27. Guillot M, Ross-Ascuitto N, Ascuitto RJ. Fluid-flow energetics for curved or angulated pathways associated with staged operations for the modified fontan procedure. Congenit Cardiol Today 2012;10:1-13.
28. Ascuitto RJ, Kydon DW, Ross-Ascuitto NT. Pressure loss from flow energy dissipation: relevance to Fontan-type modifications. Pediatr Cardiol 2001;22:110-115 .


29. Ensley AE, Lynch P, Chatzimavroudis GP, Lucas C, Sharma S, Yoganathan AP. Toward designing the optimal total cavopulmonary connection: an in vitro study. Ann Thorac Surg 1999;68:1384-1390 .


30. Stroev PV, Hoskins PR, Easson WJ. Distribution of wall shear rate throughout the arterial tree: a case study. Atherosclerosis 2007;191:276-280 .


31. Moore S, David T, Chase JG, Arnold J, Fink J. 3D models of blood flow in the cerebral vasculature. J Biomech 2006;39:1454-1463 .


 the cross-sectional area change is larger at each change of angle. In the case of a change in 90┬░, energy loss decreases to
the cross-sectional area change is larger at each change of angle. In the case of a change in 90┬░, energy loss decreases to  without a minimum value.
without a minimum value. , which is term of Bernoulli's equation.
, which is term of Bernoulli's equation. =
=  ' which represent cross-sectional area ratio.
' which represent cross-sectional area ratio. 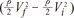 is from the Bernoulli's equation and
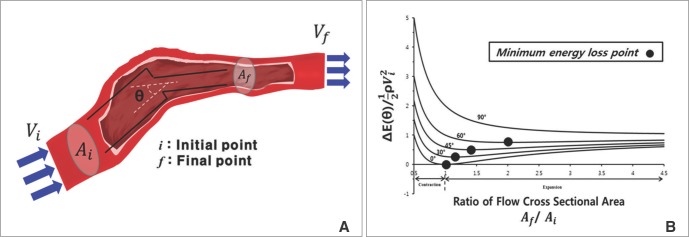
is from the Bernoulli's equation and 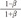 is the loss factor based on ratio of change in cross sectional area. As observed in Fig. 6A,
is the loss factor based on ratio of change in cross sectional area. As observed in Fig. 6A, 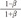 gets smaller with increasing N, meaning that the greater the cross-sectional area changes, the less the energy loss is.
gets smaller with increasing N, meaning that the greater the cross-sectional area changes, the less the energy loss is. multiplied by 'energy loss factor'. This factor decreases as N increases (Fig. 6B). To sum up, the energy loss decreases as the angle change becomes more gradual
multiplied by 'energy loss factor'. This factor decreases as N increases (Fig. 6B). To sum up, the energy loss decreases as the angle change becomes more gradual